
문제
한수는 2차원 배열 (항상 2^N * 2^N 크기이다)을 Z모양으로 탐색하려고 한다. 예를 들어, 2*2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다.
만약, 2차원 배열의 크기가 2^N * 2^N라서 왼쪽 위에 있는 칸이 하나가 아니라면, 배열을 4등분 한 후에 (크기가 같은 2^(N-1)로) 재귀적으로 순서대로 방문한다.
다음 예는 2^2 * 2^2 크기의 배열을 방문한 순서이다.
N이 주어졌을 때, (r, c)를 몇 번째로 방문하는지 출력하는 프로그램을 작성하시오.
다음 그림은 N=3일 때의 예이다.
입력
첫째 줄에 N r c가 주어진다. N은 15보다 작거나 같은 자연수이고, r과 c는 0보다 크거나 같고, 2^N-1보다 작거나 같은 정수이다
출력
첫째 줄에 문제의 정답을 출력한다.
나의 답
알고리즘
한 좌표의 위치를 4가지 경우의 수를 이용해 재귀적으로 계속 나눌 수 있다는 것을 발견
-
몇 번째 Z인지 찾기
-
주어진 판을 1/4로 나누었을 때, 어디에 속하는 지 저장
-
1번을 나눈 묶음이 4칸짜리가 되었을 때까지 (가장 작은 Z가 될 때까지) 진행
주어진 n이 1이 될 때까지 1씩 빼가면서 하면 됨
-
-
1에서 찾은 Z 모양에서 몇번째에 속하는 지 찾기

입력이 3 1 6 일 때의 상황을 나타낸 것이다.
findLocation 함수는 n이 1이면 저장해둔 array를 return한다. 그 전까지는 n을 1씩 감소시켜가며 2^(n-1)을 기준으로 x, y 값을 비교한다. 쉽게 말해서 z모양으로 1,2,3,4로 나타내서 array에 저장한다.

findLocation 함수를 지나면 배열이 나와서 가장 작은 Z모양이 나올 때까지 해당 수가 어떤 위치에 있었는지를 나타낸다. 위의 그림에서 찾고자하는 (1,6) 위치의 22는 첫번째 주황색 테두리에서 찾을 때(2^2 기준) 2번째 위치에 있고, 두번째 빨간색 테두리에서 찾을 때(2^1 기준) 또한 2번쨰 위치에 있다. 두번째 빨간 테두리가 가장 작은 Z모양이므로 있으므로 array에 [2,2]를 저장한 후 return 한다.
그 후, calIndex 함수로 주어진 위치에 있는 수를 계산하는데, array에서 수를 하나씩 꺼내면서 4의 지수승만큼을 곱해주는 방식이다.
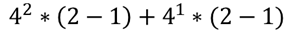
해당 식은 주황색 테두리에서 2번째에 위치했으므로 4^2만큼의 숫자가 (2-1)번 지나갔고, 빨간 테두리에서 2번째에 위치했으므로 4^1만큼의 숫자가 (2-1)번 지나갔음을 의미한다.
여기까지 계산하면 바로 전 Z모양까지의 수를 구한 것이다. 현재 Z모양에서 해당 위치가 어떤 수를 나타내는 지 알려면 Z상에 어느 쪽에 위치하는지 파악해야한다. 이는 주어진 r, c를 가지고 판단을 할 수 있다.

r,c가 모두 짝수이면 Z모양의 첫번째에 위치하므로 0을 더해주고, Z모양을 따라서 1씩 추가되는 개념이다. 이 덧셈까지 마치면 우리가 원하는 해당 위치에 해당하는 수가 출력된다.
코드
import math
N,c,r = map(int,input().split()) #c: y, r: x
def findLocation(loc_index,x,y,n): # 위치 정보 반환
if n==1: # 가장 작은 Z모양일 때
return loc_index
location = 0
if x<pow(2,n-1):
if y<pow(2,n-1):
location = 1
else:
location = 3
y-=pow(2,n-1)
else:
if y<pow(2,n-1):
location = 2
x-=pow(2,n-1)
else:
location = 4
x-=pow(2,n-1)
y-=pow(2,n-1)
loc_index.append(location)
return findLocation(loc_index,x,y,n-1)
def calIndex(loc_index,n,sum):
if n!=1:
for i in range(n-2,-1,-1): # 몇번째 Z인지
sum+=int(pow(4,n-i-1)*(loc_index[i]-1))
if r%2: # Z상의 위치 파악
if c%2:
sum+=3
else:
sum+=1
else:
if c%2:
sum+=2
#else:sum+=0
return sum
location_array = list()
location_array = findLocation(location_array,r,c,N)
if len(location_array)==N-1:
print(calIndex(location_array,N,0))
else:
print("error")시간 복잡도
재귀함수가 있으므로 최악의 시간복잡도를 구해보자. 입력 N이 15이하이므로, 15일 때 findLocation 함수에서 재귀가 14번 실행된다. 이 경우가 최악이고 calIndex 함수는 for문이 O(1)이므로 계산할 필요가 없다.
N을 15로 두고 돌렸을 때, 0.02s 소요되었다.
메모리 사용
N을 15로 두고 돌렸을 때, 9128KB 소모되었다.
느낀 점
경계값으로 제출 전 테스트 해보는 것은 필수인 듯하다.
'Algorithm 문제 > BOJ' 카테고리의 다른 글
| [python]백준 5620번 : 가장 가까운 두 점의 거리 (0) | 2020.03.01 |
|---|---|
| [python]백준 1992번 : 쿼드트리 (0) | 2020.02.29 |
| [python]백준 1019번 : 책 페이지 (0) | 2020.02.21 |
| [python]백준 4811번 : 알약 (1) | 2020.02.21 |
| [python]백준 2839번 : 설탕 배달 (0) | 2020.02.01 |

Comment