
타원곡선 DSA 디지털 서명
자료조사
DSA란?
디지털 서명 알고리즘(Digital Signature Algorithm, DSA)은 디지털 서명을 위한 표준이다. NIST가 1991년 8월 DSS라는 미국 전자서명 표준에서 이용하기 위해 정부용 전자서명 알고리즘으로 발표했으며, 현재는 DSA와 함께 ECDSA, RSA를 사용하고 있다.
디지털 서명 인증 방식
전자서명(디지털 서명)은 무결성, 인증, 부인방지를 만족해야한다.
전자서명에는 공개키 암호화 알고리즘이 쓰이며 크게 3가지 종류의 알고리즘이 있다.
- 합성수의 소인수분해문제가 어렵다는 데에 기초한 RSA형 알고리즘
- 유한체의 이산대수 문제가 어렵다는 데에 기초한 ElGamal형 알고리즘
- 타원곡선을 이용한 EC-DSA, EC-KCDSA
DSA는 이 중 ElGamal형 알고리즘으로 기밀성은 가지고 있지 않으며 전자서명 기능을 제공한다. 이러한 서명 알고리즘들은 주로 3가지 함수로 나누어 동작하며, 각각 '키 생성', '서명', '검증' 역할을 하는 함수이다.
이산대수 문제
이산 대수 문제란 Y = g^x mod p라는 문제에서 Y, g, p를 공개하더라도 x를 계산하기 어려운 문제를 뜻한다.
RSA와의 비교
디지털 서명과 인증 방식은 원래 RSA 공개키 암호화시스템을 이용하고 있었다. RSA와 DSA의 차이점은 다음 그림과 같다.
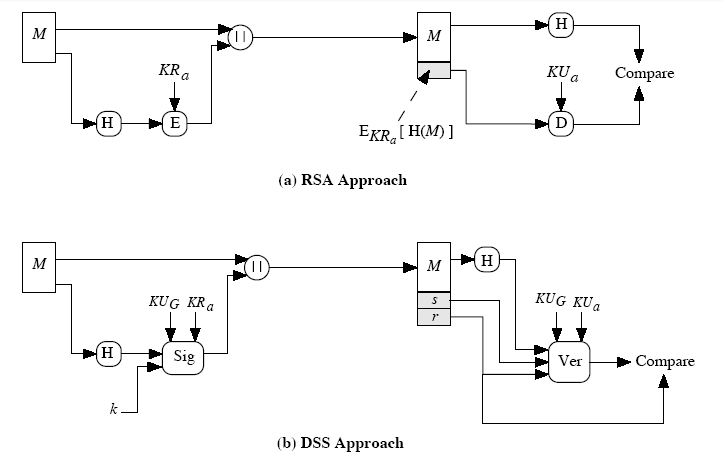
RSA는 개인키로 전자 서명 값을 만들지 않고, 원본 메시지를 압축 함수로 압축한 후 압축 해시값을 암호화하여 전자서명 값을 만든다. 메시지 인증 시에는 메시지를 다시 압축 해시값으로 만들고, 복호화된 전자서명 값과 비교하여 인증할 수 있다.
DSA도 메시지의 압축 값을 암호화해서 전자서명을 만드는 것은 같지만 메시지 인증과정이 다르다. DSA 알고리즘은 전자서명만을 위한 알고리즘이므로 비교없이 바로 인증이 가능하다.
RSA보다 키 생성, 복호화(검증) 과정이 빠르며 암호화(서명) 과정은 비교적 느린 편이다.
특징
- RSA보다 키 생성이 빠르다.
- 검증속도는 RSA보다 느리다.
- 이산 대수 문제의 어려움을 이용한 방법이다.
- 320bit 서명을 만들어 낸다.
- 해시 함수로는 SHA1을 이용한다.
문제점
Nonce reuse 문제가 있다. 서명 생성 과정에서 쓰인 k 값을 다시 사용하는 것이다. k값이 같을 때의 두 서명 (r,s1), (r,s2)가 있다고 하면
s1 − s2 = k^(−1)(H(m1)+xr−H(m2)−xr) = k^(−1)(H(m1)−H(m2))(mod q)이므로
k = (H(m1)−H(m2))/(s1−s2)(mod q)를 통해 k를 복구할 수 있다. k값을 복구하면 이를 이용해 s1, r, H(m1), k를 구해서 비밀키 x를 복구할 수 있다.
알고리즘 분석
과정
준비
-
키 길이를 정한다.
L, N을 정해야하며 일반적으로 (1024, 160), (2048, 224), (2048, 256), (3072, 256) 중 하나이다.
-
메세지 해싱 함수 H를 정의한다.
H의 output 길이는 N 이상이어야한다.
-
서명의 매개변수 (p,q,g)를 공유한다.
p값은
2^(L-1) < p < 2^L를 만족하며 L bit 길이인 소수이다.q값은
2^(N-1) < q < 2^N을 만족하며 N bit 사이의 길이를 가진 수이다.=> 여기서 p-1이 q의 배수여야한다.
g값은
g = h^((p-1)/q) mod p를 만족하며1 < q < p인 수이다.이 때,
1 < h < p-1 && g > 1이고 일반적으로 h는 2를 고른다.
키 생성
-
공개키 y를 생성한다.
0 < x < q인 x(개인키)를 꼽은 후,y=g^x mod p로 공개키인 y를 계산한다.이산대수 문제로 y값으로부터 x를 쉽게 구할 수 없다.
서명 생성

-
랜덤한 수를 생성한다.
0보다 크고 q보다 작은 랜덤 수 k를 생성한다.
-
전자 서명을 한다.
r = (g^k mod p) mod q s = (k^(-1)(H(M) +xr)) mod q -
(r, s, M)을 전송한다.
서명 검증
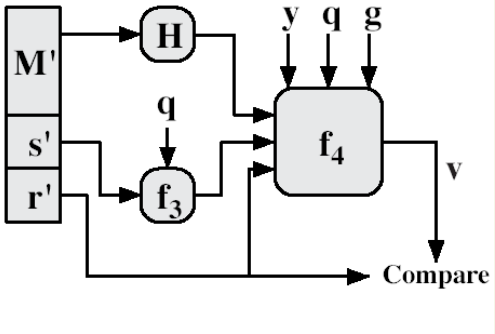
-
(r, s, M)을 받는다.
-
값을 계산한다.
w = s^-1 mod q u1 = (H(M)w) mod q u2 = rw mod q v = ((g^u1*y^u2) mod p ) mod q -
v가 r이라면 인증 완료이다.
Correctness of the algorithm
알고리즘에서 g = h^((p-1)/q) mod p이었으므로 g^q = h^(p-1) = 1 mod p이다. 따라서 a = b (mod q) 인 조건에서 g^a = g^b (mod p)가 성립함을 알 수 있다.
위의 알고리즘에서 s = (k^(-1)(H(M) +xr)) mod q 이므로 위의 성질을 이용하면 k = (s^(-1)(H(M) +xr)) mod q로 나타낼 수 있다. 따라서
r = (g^k mod p) mod q = ((g^u1*y^u2) mod p) mod q = v이기 때문에 알고리즘이 성립한다.
프로그램 구현
언어는 C++로 IDE는 Visual Studio를 이용하여 구현하기로 한다.
주요 코드 구성
코드는 송신자인 Sender와 수신자인 Receiver class로 나누어 구현하였으며, 중간을 매개하는 main함수는 서비스 제공 시스템이라고 보면 된다.
Sender 클래스는 4가지 함수로 이루어져있으며, 각 함수에서 쓰이는 변수들은 private으로 선언되어있다.
먼저 송신자는 initialize 함수를 이용하여 지정된 해시함수를 이용한 메세지의 해시값, 변수 길이 결정 변수, 매개변수들을 세팅하는 역할을 한다. 그 후 generateKey 함수를 이용하여 해당 매개변수들로 비밀키 x와 공개키 y를 만들어낸다. 해당 함수에서 호출되는 generateSign으로 서명을 만들어내고, 서명이라고 일컫는 r과 s를 sendRS 함수로 Receiver에게 보낸다.
Receiver 클래스는 verifySign이라는 하나의 함수로 이루어져있다. Sender와 마찬가지로 필요한 변수들은 private으로 선언되어있다.
수신자는 전달받은 r, s, M을 가지고 검증을 시작한다. 계산 결과 도출된 v 변수 값과 송신자로부터 받은 r값이 같으면 서명이 일치하므로 검증이 완료되고 전달받은 메세지를 출력한다. 같지 않다면 검증에 실패한다.
도움 함수
전역 구간에 존재하는 두 가지 도움함수가 있다. bigModuler 함수는 unsigned long의 범위를 벗어나는 모듈러 계산을 위해 재귀함수의 형태로 분할정복하는 함수이다. isPrime 함수는 해당 변수가 소수인지를 판단하는 도움함수로 매개변수 p값을 결정할 때 사용된다.
헤더파일
헤더파일로는 Euclid.h와 SHA1.h가 있다. 코드 상에서 사용되는 해시 함수는 직접 구현해둔 SHA1 함수를 사용하였다.
또한 알고리즘 중 모듈러 곱의 역원을 구하는 부분이 있는데, 이를 구현하려면 2가지 방법을 사용할 수 있다.
-
순차적으로 증가하면서 역원 찾기
-
확장된 유클리드 호제법 이용하기
본인은 처음에 1번 방법을 이용하여 코드를 구현하였으나, 역원을 찾는 데에 시간이 너무 오래 걸려서 유클리드 호제법을 구현한 Euclid.h 파일을 만들었다.
부족한 점
위의 알고리즘 분석 파트에서 설명했듯이 L과 N은 주어진 bit 쌍이 존재한다. L은 최소 1024bit 부터 시작하므로 계산의 범위가 너무 커져 다루기가 어려웠다. 따라서 본인은 L과 N을 낮은 수로 고정해둠으로써 unsigned long의 범위내에서 계산 가능한 코드로 구현했다.
코드
<Euclid.h>
#include <iostream>
using namespace std;
typedef unsigned long ulong;
ulong Euclid_module(ulong, ulong);
ulong Inverse(ulong n1, ulong n2) {
int inv = 0;
if (n1 > n2)
inv = Euclid_module(n1, n2);
else
inv = Euclid_module(n2, n1);
return inv;
}
ulong Euclid_module(ulong r1, ulong r2) {
int r, q, s, s1 = 1, s2 = 0, t, t1 = 0, t2 = 1, tmp = r1;
while (r2)
{
q = r1 / r2;
r = r1 % r2;
s = s1 - q * s2;
t = t1 - q * t2;
r1 = r2;
r2 = r;
s1 = s2;
s2 = s;
t1 = t2;
t2 = t;
}
if (r1 == 1) // 역수 존재
{
if (t1 < 0)
t1 += tmp;
return t1;
}
return 0;
}<SHA1.h>
#include <cmath>
#include <vector>
#include <string>
#include <sstream>
#include <iomanip>
#include <iostream>
using namespace std;
std::string m;
uint64_t ml;
uint32_t weight[80];
uint32_t k_sha[80];
int exe = 0;
unsigned int h_sha[5] = {
0x67452301,
0xEFCDAB89,
0x98BADCFE,
0x10325476,
0xC3D2E1F0
};
unsigned int rotl32(unsigned int value, unsigned int count) {
return ((value << count) & 0xFFFFFFFF) | ((value & 0xFFFFFFFF) >> (32 - count));
}
void padding() {
// m에 padding을 추가하기 전 length (bit size)
ml = m.size() * CHAR_BIT; // m.size() => 64bit (8byte)
// 0x80 = 2^7 = 10000000
// 원래 메세지에 bit '1' 추가
// 어차피 다음 단계에서 0을 채우기 때문에 미리 7개 추가
m += (char)0x80;
// 64byte(512bit)로 나누어떨어지도록 0 채워주기
// m.size()가 64(byte)가 될 때까지
while (m.size() % 64 != 64 - sizeof(ml)) {
m += (char)0x00;
}
// 맨 뒤에는 메세지 size 넣기
// 8bit 씩
for (int i = 7; i >= 0; i--) {
char byte = (ml >> 8 * i) & 0xff;
m += byte;
}
// 이제 m은 64bytes(512bit)로 나누어 떨어진다.
}
void wSetting() {
// m을 w 처음에 채우기
// m (64byte(512bit)) => 16개의 w => 하나의 w당 4byte(4글자 = 4*char)의 m이 할당됨
for (int i = 0; i < 16; i++) {
weight[i] = (m[4 * i + 3] & 0xff)
| (m[4 * i + 2] & 0xff) << 8
| (m[4 * i + 1] & 0xff) << 16
| (m[4 * i + 0] & 0xff) << 24;
}
// weight 가공해서 나머지 weight 채우기
for (int i = 16; i < 80; i++) {
weight[i] = rotl32(weight[i - 16] ^ weight[i - 14] ^ weight[i - 8] ^ weight[i - 3], 1);
}
}
void kSetting() {
for (int i = 0; i < 20; i++)
k_sha[i] = 0x5A827999;
for (int i = 20; i < 40; i++)
k_sha[i] = 0x6ED9EBA1;
for (int i = 40; i < 60; i++)
k_sha[i] = 0x8F1BBCDC;
for (int i = 60; i < 80; i++)
k_sha[i] = 0xCA62C1D6;
}
uint32_t F(unsigned int b, unsigned int c, unsigned int d) {
if (exe < 20) {
return (b&c) | ((~b)&d);
}
else if (exe < 40) {
return (b^c^d);
}
else if (exe < 60) {
return ((b&c) | (b&d) | (c&d));
}
else if (exe < 80) {
return (b^c^d);
}
}
void SHA() {
uint32_t a = h_sha[0]; uint32_t b = h_sha[1]; uint32_t c = h_sha[2]; uint32_t d = h_sha[3]; uint32_t e = h_sha[4];
// 80번 loop
uint32_t temp;
while (exe != 80) {
temp = rotl32(a, 5) + F(b, c, d) + e + weight[exe] + k_sha[exe];
e = d;
d = c;
c = rotl32(b, 30);
b = a;
a = temp;
exe++;
}
h_sha[0] = h_sha[0] + a;
h_sha[1] = h_sha[1] + b;
h_sha[2] = h_sha[2] + c;
h_sha[3] = h_sha[3] + d;
h_sha[4] = h_sha[4] + e;
}
unsigned int SHA1(string message) {
m = message;
padding(); // 1. 메세지 padding 처리
wSetting(); // 2. w 세팅
kSetting(); // 3. k 세팅
SHA(); // 4. SHA
unsigned int result=0;
for (int i = 0; i < 5; i++) {
result += h_sha[i];
}
return result;
}<DSA.cpp>
#include <iostream>
#include <random>
#include <math.h>
#include <Windows.h>
#include <vector>
#include "SHA1.h"
#include "Euclid.h"
using namespace std;
typedef unsigned long ulong;
random_device rd;
mt19937 gen(rd());
ulong p, q, g;
ulong y;
ulong Hm;
string M;
ulong bigModuler(ulong n, ulong e, ulong m) { // 큰 수의 모듈러 계산을 위한 함수
if (e <= 3) {
return ((int)pow(n, e)) % m;
}
if (e % 2 == 0) { // 짝수이면
ulong tmp = bigModuler(n, e / 2, m);
return (tmp*tmp) % m;
}
else {
ulong tmp = bigModuler(n, (int)e / 2, m);
ulong tmp2 = bigModuler(n, e-(int)e / 2, m);
return (tmp*tmp2) % m;
}
}
bool isPrime(ulong num) { // 소수를 판별하기 위한 함수
for (int i = 2; i <= (int)sqrt(num); i++) {
if (num%i == 0)
return false;
}
return true;
}
class Receiver {
private:
ulong w, u1, u2, v;
public:
void verifySign(ulong r, ulong s) { // 전자서명 인증 과정
cout << "verifying..." << endl;
ulong inv_s = Inverse(s, q);
w = inv_s % q;
u1 = (Hm*w) % q;
u2 = (r*w) % q;
v = ((bigModuler(g,u1,p)*bigModuler(y,u2,p)) % p) % q;
if (v == r) { // 서명이 일치하면 통과 => 메세지 출력
cout << "authentication success :>" << endl;
cout << "message : " << M << endl;
}
else {
cout << "authentication denied :<" << endl;
}
}
};
class Sender {
private:
ulong L, N;
ulong h = 2;
ulong k, r, s;
public :
vector<ulong> sendRS() {
cout << "sending..." << endl;
vector<ulong> rs;
rs.push_back(r);
rs.push_back(s);
cout << "send complete!" << endl << endl; // r,s,M 전송
return rs;
}
void generateSign(ulong x) {
uniform_int_distribution<> dis4(1, q - 1);
k = dis4(gen); // 랜덤 수 k 생성
ulong inv_k = Inverse(k, q);
r = bigModuler(g, k, p) % q;
s = (inv_k*(Hm + x * r)) % q;
if (s == 0) { // s가 0이면 다시 하기
generateKey();
}
}
void generateKey() {
uniform_int_distribution<> dis3(1, q - 1);
ulong x = dis3(gen); // 랜덤 수 x 생성
y = bigModuler(g, x, p);
generateSign(x); // 전자서명 생성
}
void initialize() {
L = 5; N = 2; // length 설정
Hm = SHA1(M); // 해시 함수 이용 => 메세지 해시값 생성
uniform_int_distribution<> dis((ulong)pow(2, L - 1) + 1, (ulong)pow(2, L) - 1);
do {
p = dis(gen);
} while (!isPrime(p)); // 주어진 범위 내의 소수 p 찾기
int flag = 0;
for (ulong i = (ulong)pow(2, N - 1) + 1; i >= (ulong)pow(2, N) - 1; i--) {
if ((p - 1) % i == 0) {
q = i;
flag = 1;
}
}
if (!flag) {
initialize();
}
g = bigModuler(h, (ulong)((p - 1) / q), p);
}
};
int main() {
cout << "문자열을 입력해주세요." << endl;
cin >> M;
cout << endl;
Sender* s = new Sender(); // 수신자 생성
Receiver* r = new Receiver(); // 송신자 생성
s->initialize(); // 초기화
s->generateKey(); // 키 생성
cout << "공개키 : " << y << endl; // 공개키 공개
vector<ulong> tmp = s->sendRS(); // r,s,M 전송
r->verifySign(tmp[0],tmp[1]); // 전자서명 인증
cin >> M;
}실행화면

시스템을 시작하고 문자열을 입력하면 공개키가 출력된다. Sender가 Receiver에게 보내는 과정이 지난 후, Receiver가 검증할 때, 주어진 공개키와 전달받은 매개변수를 가지고 검증절차를 거친다. 검증에 성공하면 성공표시와 함께 Sender가 보낸 메세지가 출력된다.
참고문헌
https://www.nist.gov/publications/digital-signature-standard-dss-0?pub_id=902984
http://blog.naver.com/PostView.nhn?blogId=turbo0815&logNo=60049190798
http://www.parkjonghyuk.net/lecture/modernCrypto/lecturenote/chap09-1.pdf
http://www.secmem.org/blog/2019/07/21/Digital-Signature-and-Nonce-Ruse/
https://eunplay.tistory.com/122
http://www.secmem.org/blog/2019/07/21/Digital-Signature-and-Nonce-Ruse/
https://blog.naver.com/techshare/220921626310
https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.186-4.pdf
'컴퓨터과학 (CS) > Computer Security' 카테고리의 다른 글
| [컴퓨터 보안] 근대 암호방식 (SEED, SSL, RSA) 정리 (0) | 2020.04.12 |
|---|---|
| [컴퓨터 보안] 해시함수 (정의, 효과, 용도, 종류, 구현, 약점) (0) | 2020.04.08 |
| [컴퓨터 보안] 치환 암호 vs 전치 암호 :: 주상전치암호 (0) | 2020.04.08 |

Comment