
7. 분할 정복
7.1 도입
분할 정복( Divide & Conquer)은 가장 유명한 알고리즘 디자인 패러다임으로, 각개 격파라고 설명할 수 있음
주어진 문제를 둘 이상의 부분 문제로 나눈 후, 재귀 호출을 이용해 각각의 답을 계산하고, 부분 문제의 답을 이용해 전체의 답을 계산하는 방식
알고리즘 구성
-
divide
문제를 더 작은 문제로 분할
-
merge
각 문제의 답을 전체 문제의 답으로 병합
-
base case
더이상 답을 분할하지 않고 풀 수 있는 매우 작은 문제
적용가능한 문제의 특성
- 문제를 부분 문제로 나누는 자연스러운 방법이 존재해야함
- 부분 문제의 답을 조합해 전체 문제의 답을 계산하는 효율적인 방법이 있어야함
장점
대부분의 경우에서 작업을 빠르게 처리해줌
예제 : 수열의 빠른 합과 행렬의 빠른 제곱
1에서 n까지의 합을 계산
-
재귀함수를 이용
def Sum(num): if num == 1: return 1 return num+Sum(num-1) -
분할 정복 이용
1~n의 합은 1~2/n의 합에다가 2/n~n의 합을 더한 것과 같음
2/n~n의 합은 1~2/n의 합 + 2/n*2/n 이므로 한번의 재귀로 나타낼 수 있음
def Sum(num): if num == 1: # 짝수일 때 2/n 하다보면 도달 return 1 if num%2 == 1 : # 홀수일 때는 return Sum(n-1)+n return Sum(2/n)+(2/n)*(2/n)
무엇이 더 나을까?
재귀는 n번의 함수 호출이 필요
분할정복은 2/n보다 약간 큰 수의 함수 호출 예상
분할정복에서 흐름을 글로 나타내보면
- 홀수인 경우에는 현재 수+ 재귀(현재 수에서 1을 뺀 짝수)
- 짝수인 경우에는 재귀(현재 수를 2로 나눈 짝수)+상수
이므로 재귀로 넘어가는 n은 각각
- 1을 뺀다.
- 2로 나눈다.
이다.
이를 2진수로 표현해보면, 어떤 수 N의 이진수 표현 끝자리가 1인 경우는 홀수이므로 끝자리를 0으로 바꾸게 만들고 0인 경우는 짝수이므로 끝자리 하나를 지우는 것이 재귀로 넘기는 방법이다. 이에 더해 현재 수와 상수가 각각 붙지만 함수가 몇 번 실행될 지만 따지면 되기 때문에 이러한 방식으로 구할 수 있다.
2진수로 표현했을 때 자리 수 + 첫 자리를 제외하고 나타나는 1의 개수가 함수의 총 호출 횟수이다.
두 값의 상한은 모두 logn이다.
logn = log(2)n
따라서 이 알고리즘의 실행시간은 O(logn)이다.
행렬의 거듭 제곱
행렬의 거듭 제곱을 그냥 계산하려고 구현하면 n*n 행렬의 m승 거듭제곱을 구하는데에 O(n^3*m) 의 시간이 걸린다.
분할 정복을 이용해보자.
절반으로 잘라서 A의 m승을 (A의 m/2승)*(A의 m/2승) 으로 만드는 방법이다.
matrix # 2차원 행렬
def pow(matrix, m): # matrix의 m승을 반환하는 함수
if m==0 # 기저 사례 : A의 0승
return 1
if m%2==1: # 홀수일 때
return pow(matrix,m-1)*matrix
half = pow(matrix,m/2)
return half*half나누어 떨어지지 않을 때의 분할과 시간 복잡도
m이 홀수일 때 matrix*재귀(m-1) 보다 재귀(m-1/2)*재귀(m+1/2) 이렇게 나누는 것이 더 낫지 않을까?
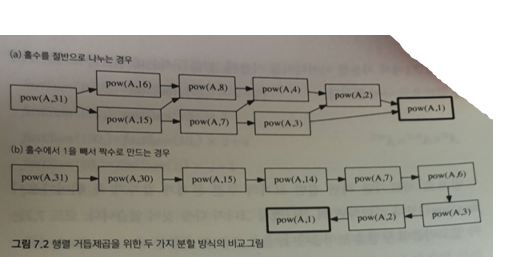
중복해서 계산되는 부분이 있음
부분 문제가 중복되는 문제는 계속 다뤄질 것임!
예제: 병합 정렬과 퀵 정렬
- 병합 정렬 : 주어진 수열을 가운데에서 쪼개 이들을 재귀 호출을 이용해 각각 정렬
- 퀵 정렬 : 주어진 수열을 파티션 단계를 거쳐 하나의 수를 기준으로 양쪽 수열로 나누는 방식으로 정렬

둘다 같은 문제를 해결하는 같은 패러다임(분할 정복 패러다임)을 이용한 알고리즘이지만, 서로 다르다.
시간 복잡도 분석
-
병합 정렬
병합 정렬에서는 나뉘어진 부분 문제에서 해답을 반환하는 방식으로 진행된다. 하나의 원소를 가진 수열으로 다 나누어진 단계 이후부터는 병합 단계이기 때문에 각 수열의 모든 원소를 거쳐서 크기 비교 후 삽입해야하는데, 모든 원소를 거치는 과정이 n번으로 항상 같다. 즉, 각 단계(그림에서 표현된 가로줄)는 항상 같은 원소의 수를 가지고 있다. 따라서 n개의 원소를 합치는데에는 logn 만큼의 단계에서 n만큼의 반복문을 돌면서 정렬해야하므로, 병합 정렬의 시간 복잡도는 O(nlogn)이다.
-
퀵 정렬
퀵 정렬의 파티션 과정은 병합 정렬의 병합 과정과 비슷하지만, 두 수열이 비슷한 크기로 나눠진다는 보장이 없기 때문에 시간 복잡도를 계산하기 힘들다. 따라서 최악의 시간복잡도가 나오는 상황을 보면, 기준으로 한 수가 최대나 최소의 수일 때이다. 이러한 경우 퀵정렬의 시간 복잡도는 O(n^2)이다. 하지만 평균적으로 계산하면 병합정렬과 같은 O(nlogn)이 된다는 것이 알려져 있다. 따라서 퀵 정렬을 구현할 때는 가능한 절반에 가까운 분할을 얻기 위한 방법을 사용한다.
예제: 카라츠바의 빠른 곱셈 알고리즘
: 분할 정복 알고리즘의 한 예
두 개의 큰 정수를 곱하는 알고리즘
- 단순 알고리즘

이러한 초등학교 때 썼던 알고리즘을 그대로 구현했을 때, 큰 수가 담겨있는 배열을 2중 for문으로 접근해야하므로 O(N^2)의 복잡도가 나온다.
- 카라츠바 알고리즘
큰 수가 2개를 반 씩 자리수를 나누어서 표현
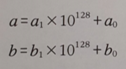
a1 = 앞의 128자리, a0 = 뒤의 128자리
이런 표현 방식으로 a*b를 표현하면

이렇게 a0,a1,b0,b1 네 가지의 조각으로 표현할 수 있는데 이때는 시간 복잡도가 O(N^2)으로 같다. 이를 3가지로 뭉쳐서 z0,z1,z2 세가지 조각으로 표현하면 시간 복잡도에서의 효율을 높일 수 있다는 것이다.
z1을 (a0+a1)*(b0+b1)-z0-z2 로 표현한다면 곱셈 세 개로 세 조각을 표현할 수 있으므로 시간 복잡도가 낮아진다.
알고리즘
- a, b를 받는다. (더 큰 수를 a로 둔다.)
- O(n^2)의 일반적 알고리즘을 해도 괜찮을 입력 범위면, 기본 알고리즘을 계산해서 return 한다.
- a와 b를 반으로 나눠서 a0,a1,b0,b1을 만든다.
- 3번에서의 네 가지 변수로 z0,z1,z2를 만든다. (재귀 함수 이용)
- 세 가지 변수로 마지막 식을 만들어서 return 한다.
시간 복잡도
n = 2^k 일 때, k번 재귀 호출 하면서 마지막에 3번의 곱셈 필요
총 3^k번의 곱셈 필요 => 3^(lgn)
O(3^(logn))=O(n^(log3))
log3은 1.585 정도이므로 n^2보다 적은 시간복잡도임
*주의 : 입력의 크기가 작은 경우 O(n^2)보다 느릴 수 있음
'Algorithm 문제 > 알고리즘 문제해결전략' 카테고리의 다른 글
| [python] 알고리즘 문제 해결 전략 1권 :: 팬미팅 (ID: FANMEETING) (0) | 2020.03.16 |
|---|---|
| [python] 알고리즘 문제 해결 전략 1권 :: 쿼드 트리 뒤집기 (189p) 문제 (0) | 2020.02.29 |
| [python] 알고리즘 문제 해결 전략 1권 :: 시계 맞추기 (p168) 문제 (0) | 2020.02.15 |
| [python] 알고리즘 문제 해결 전략 1권 :: 게임판 덮기 (p159) 문제 (0) | 2020.02.14 |
| [python] 알고리즘 문제 해결 전략 1권 :: 소풍 (p155) 문제 (0) | 2020.02.12 |

Comment